Type-safe scripting with C++ (and other weird explorations)
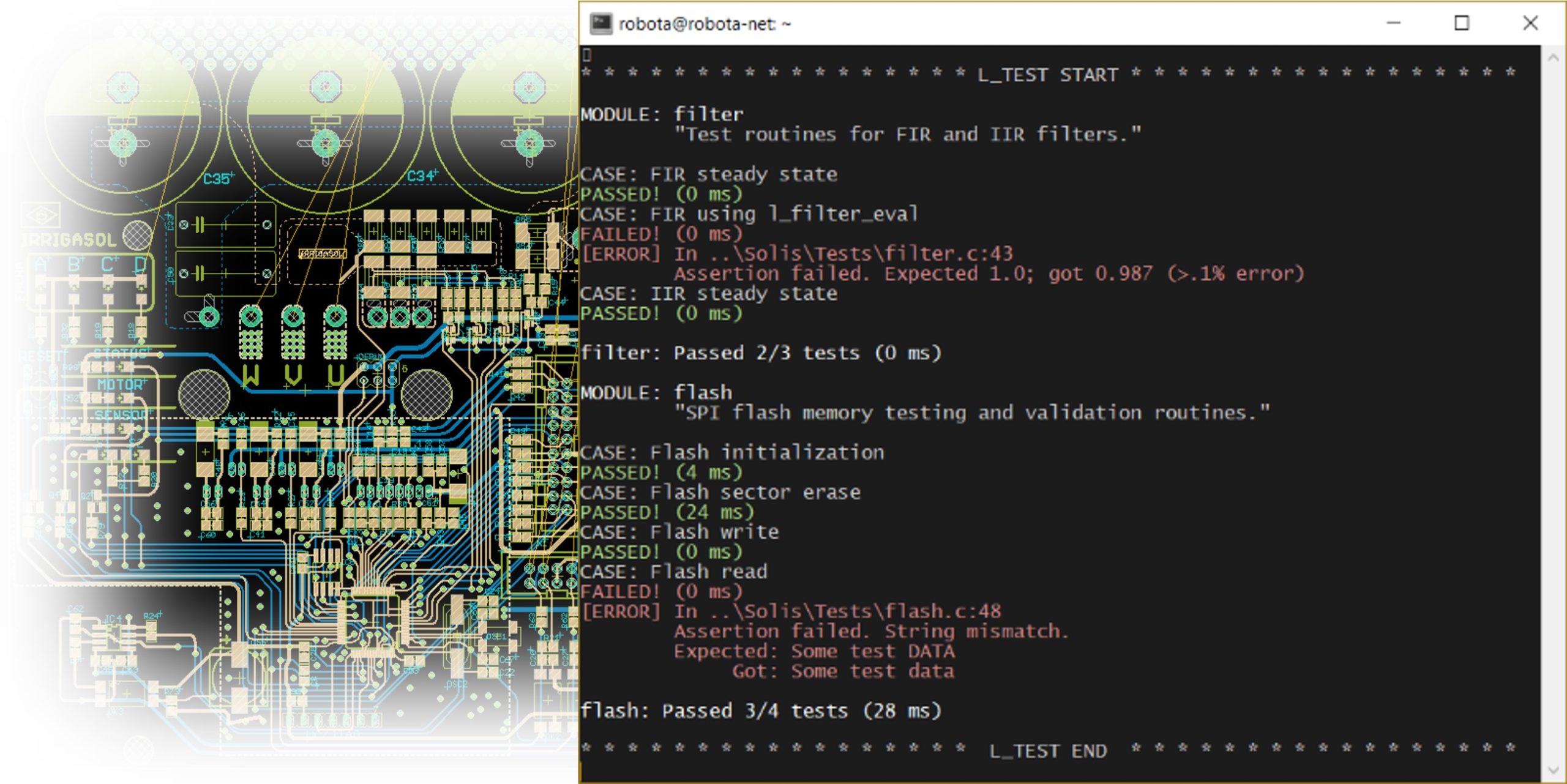
The why and the what(-the-f***) Let’s start this short tale with some background. For reasons unclear, I’ve started working on my n-th abandonable side-project. Much detail isn’t necessary here: it’s basically a C++ library for performing simple math operations— averaging, sum, standard deviation, autocorrelation and the like. Each operation is implemented as Functor: instantiate it, … Read more