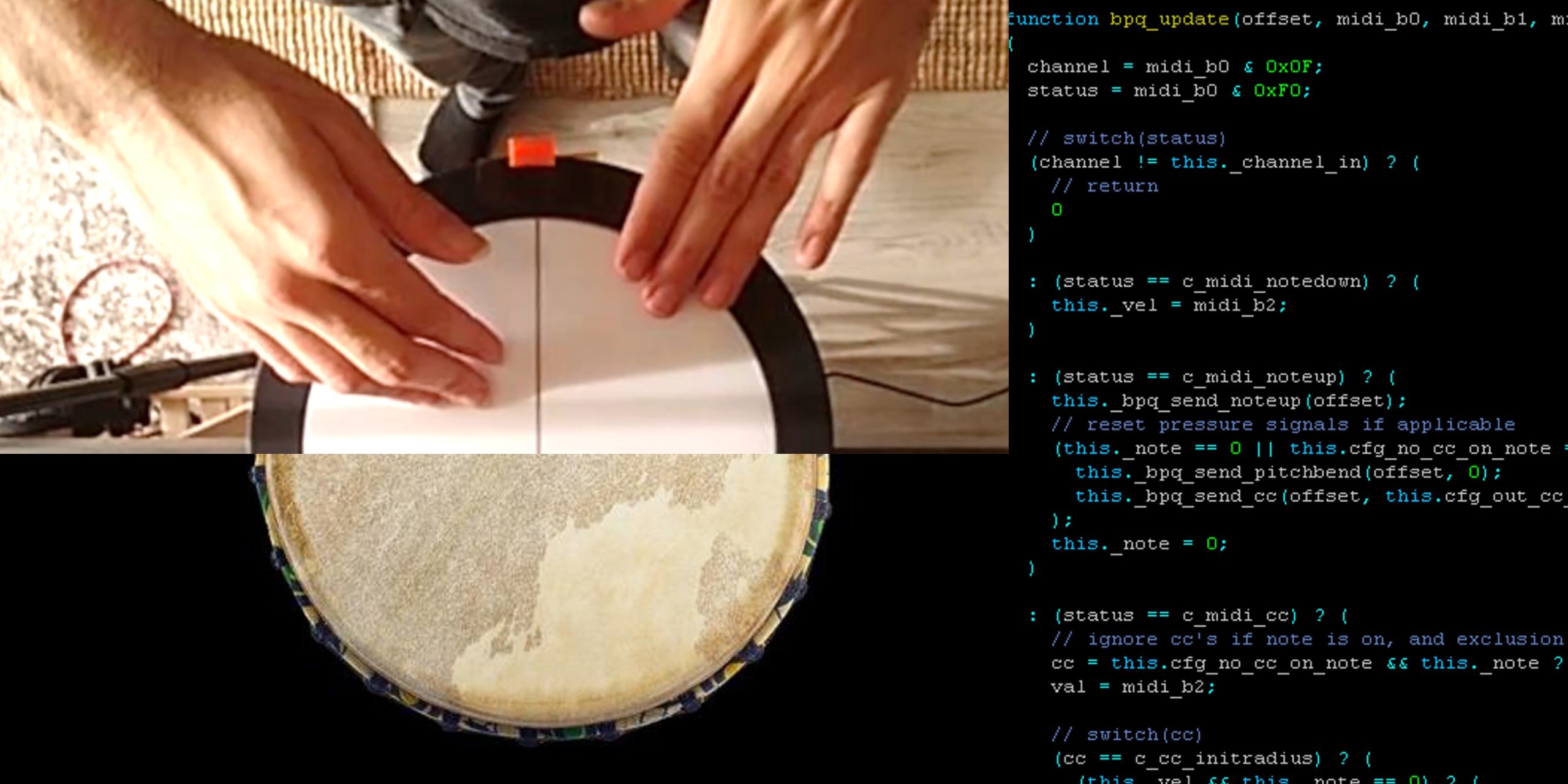
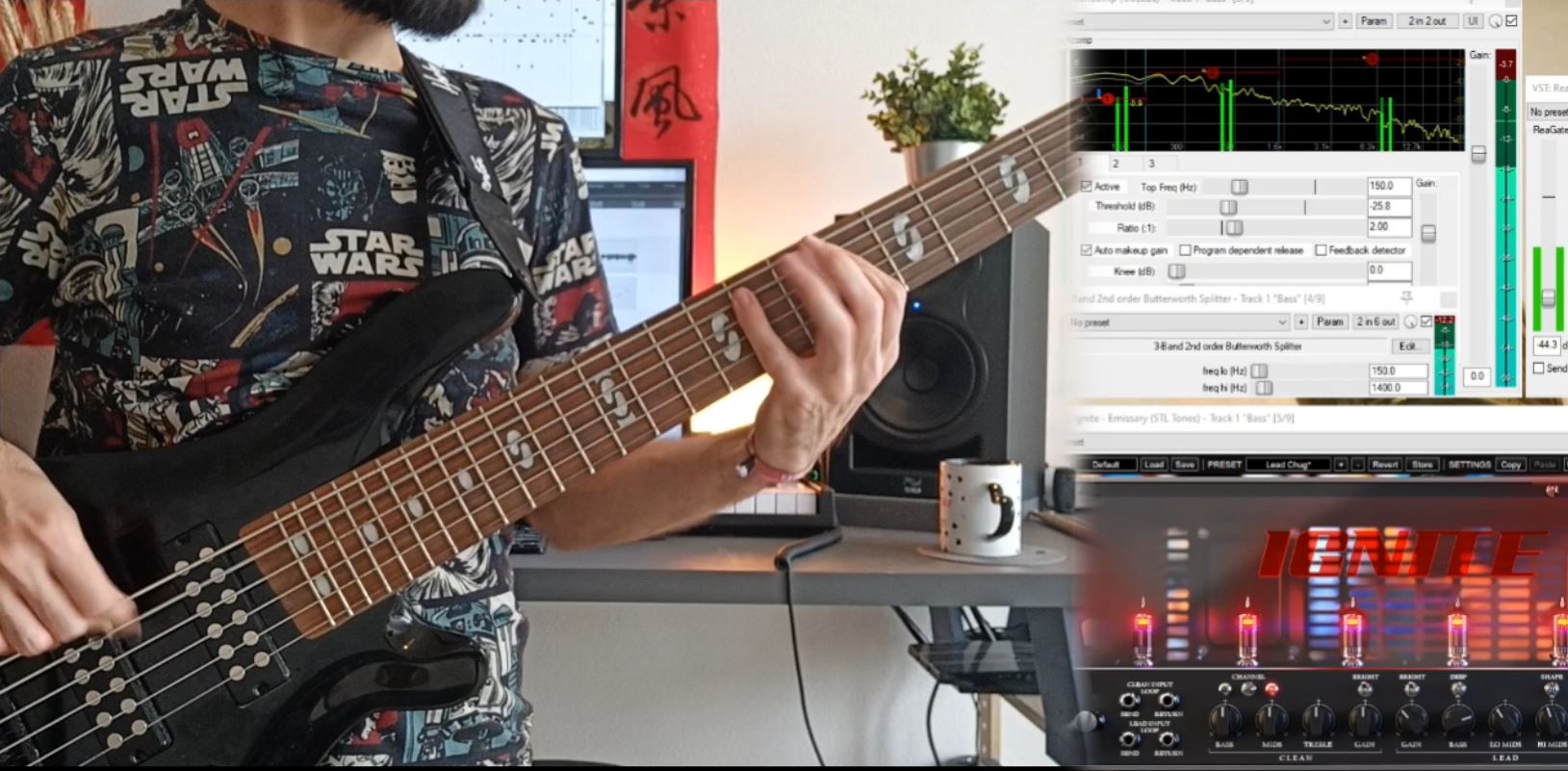
Analog-to-digital percussions
tl;dr: jump to the end for a video where I hit a thing that sounds like other things. Percussions are as cool as they are broadly defined. Hit a thing once – that’s noise. Hit it again rhytmically – that’s percussion. The constraint is, you need an it to hit: a drum, cymbal, triangle, tambourine, … Read more