Following my last post on my minimalist filter library, I just got off my butt to add some high-pass filtering capabilities too. That’s specially useful when you’re trying to remove trends from datasets – this happens a lot for instance in biomedical applications, e.g. ECG, where some breathing artifacts come up as low frequency trends on your signal.
A simple example of such trend removal is included. As shown in the snippet below, taken from the example, after instancing the Filter, extracting the trend and DC components is very straigthforward:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Filter fhp(cutoff_freq, sampling_time, IIR::ORDER::OD2, IIR::TYPE::HIGHPASS); // ... void loop() { // Composing a fast (10hz) signal over a slow one (~0.4hz, trend), both with DC components for(int r=0; r<10; r++) { sign_raw = 3.0*(float)sine12bits_256samples[s1i] + sine12bits_100samples[s2i]; s2i = ++s2i % 99; // High-pass filter removes low frequency trend and DC component sign_filt = fhp.filterIn(sign_raw); // Loop time has to be approximately equal to selected sampling period delay(1); // View with serial plotter // ... } s1i = ++s1i % 255; } |
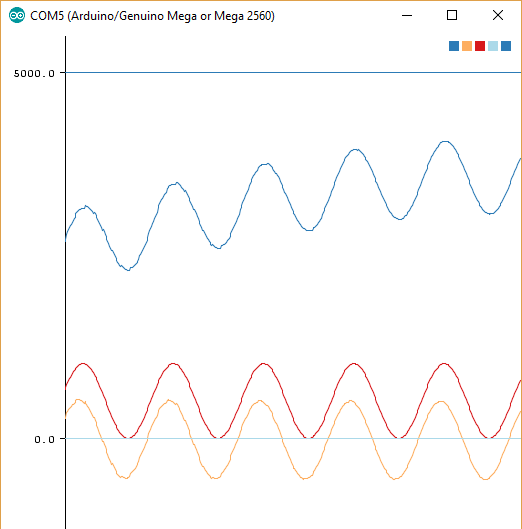
The result looks like the following (blue senoidal wave on top is signal + trend + DC, red senoid is signal + DC, orange senoid is the filtered signal):
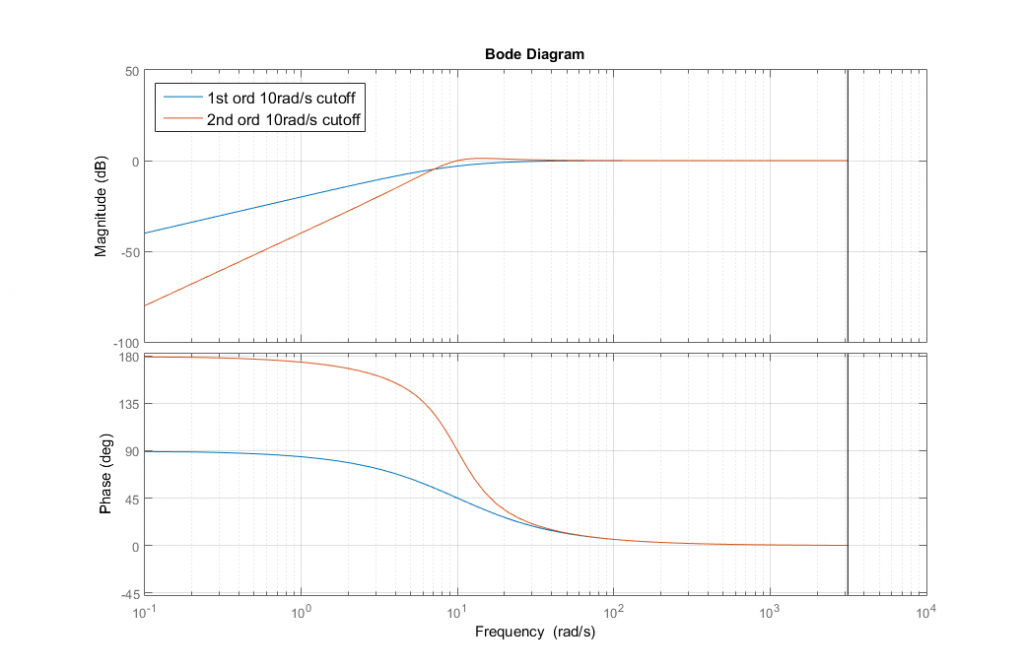
The filters implemented go only up to order 2 (I was lazy, sorry), and are also based on normalized Butterworth polynomials, discretized via Bilinear Transforms. Frequency responses for two hypotetical filters at 1kHz sampling frequency are shown below:
All filters are implemented in closed forms, so they can be reparameterized on the fly with minimum computational effort. Enjoy (and report any bugs). Major cleanup on the code is foreseen (and a notch-filtering example too).
’til next time.